1 분 소요

Maxout이란

Maxout은 특정 유형의 신경망 레이어로서 기존 활성화 함수(ReLU, Sigmoid, etc.)등을 사용하는 대신, Maxout Layer로 들어온 입력값 중에서 가장 큰 값을 선택하여 사용하는 방식입니다.

Formula of Maxout

$h(x) = \max(W_{1}\cdot x + b_{1}, W_{2}\cdot x + b_{2},\,..., W_{n}\cdot x + b_{n})$

$h(x) = \max(Z_{1},Z_{2},\,...,Z_{n})$

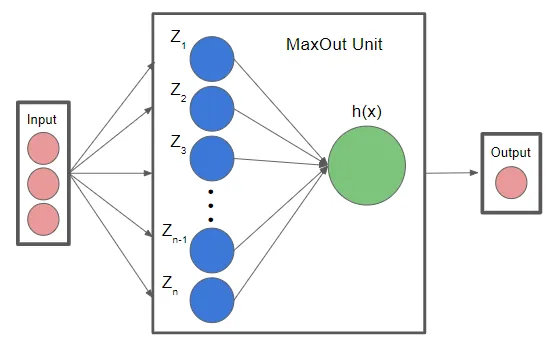
maxout

여기서 $W_{1},\,W_{2},\,W_{n}$는 뉴런에 대한 가중치 백터이고, $b_{1},\,b_{2},\,b_{n}$는 bias입니다. 여기 n 항 중에서 가장 큰 값을 선택하게 되므로, 뉴런은 입력값에 대해 두 가지 다른 선형 함수 중 하나를 선택하게 됩니다.

Maxout Illustration

maxout-illustration

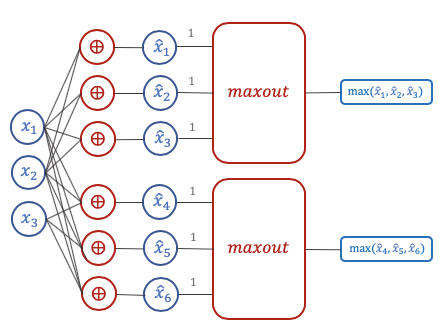
다음 그림을 보면 그룹을 나누어서 $\hat{x_{1}} = Z_{1}$ 이니깐 $\hat{x_{1}},\, \hat{x_{2}},\, \hat{x_{3}}$을 하나의 그룹으로 묶어서 maxout으로 묶고, $\hat{x_{4}},\, \hat{x_{5}},\, \hat{x_{6}}$을 따로 또 maxout으로 묶으면 각각의 maxout은 $\max(\hat{x_{1}},\, \hat{x_{2}},\, \hat{x_{3}})$으로 나온 값 하나와 $\max(\hat{x_{4}},\, \hat{x_{5}},\, \hat{x_{6}})$에서 나온 값 총 2개가 다음 Layer로 전파되게 됩니다.

Example of Maxout

  • Input = [2(batch), 5(input)]
  • Weights = [12(unit), 5(input)]
  • Biases = [12(unit)]
  • Z = [2(batch), 12(unit)] -> [2(batch), 4(maxout), 3(input of each maxout)]
  • O = max(Z, axis=2) = [2(batch), 4(maxout)]

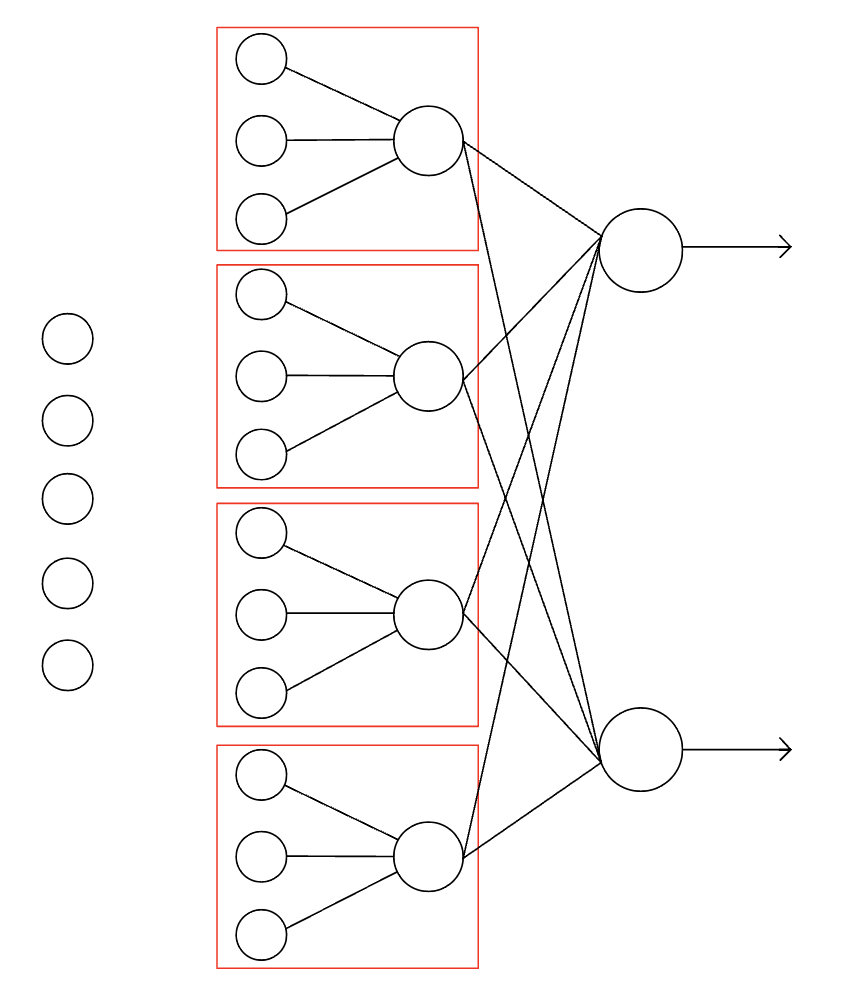
maxout_example

Implementation of Maxout

위에 예시를 파이썬 코드로 구현한 것입니다.

import numpy as np

# 5 Input size
x = np.random.random((2, 5))
print('Input shape:',x.shape)

# 12 hidden neurons
W = np.random.random((12, 5))
b = np.random.random((12))
print('Weight size:',W.shape,'biases:', b.shape)
z = np.dot(x, W.T) + b
print('z shape:', z.shape)

# 4 maxout
z_ = z.reshape((2, 4, 3))
o = np.max(z_, axis=2)
print('Output:', o.shape)

Input shape: (2, 5)
Weight size: (12, 5) biases: (12,)
z shape: (2, 12)
Output: (2, 4)

Conclusion

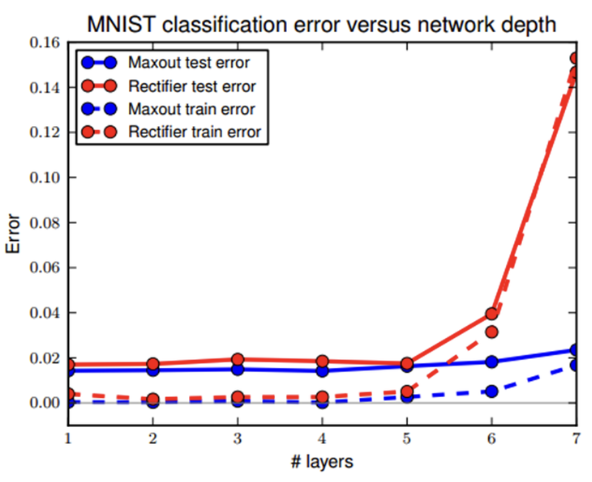
maxout_relu

  • ReLU는 입력이 음수인 경우에는 오차 역전차 과정에서 그래디언트가 0이 되기 때문에 소실되는 문제가 발생하였지만 Maxout은 항상 입력 중에서 가장 큰 값을 선택하기 때문에, 입력이 음수인 경우에도 항상 그레디언트를 전달할 수 있어서 이러한 문제를 완화할 수 있습니다.

참고