2 분 소요

Histogram Equalization이란

일반적으로 이미지는 각각의 픽셀들을 가지고 있는데 그때 해당 픽셀 값의 분포를 나타내는 그래프 표현이 Histogram(히스토그램)이고, 해당 히스토그램은 주로 어두운 픽셀값과 밝은 픽셀 값을 가지고 있습니다. 따라서 이때 이 히스토그램을 균일하게 하여 어두운 영역과 밝은 영역의 대비가 더욱 뚜렷해지면서 이전보다 더욱 뚜렷한 이미지를 얻을 수 있게 됩니다.

Formula of Histogram, Normalized Histogram

$h(l) =$ |{$(j,i)|f(j,i) = l$}|

$\hat{h} = \frac{h(l)}{M\times N}$

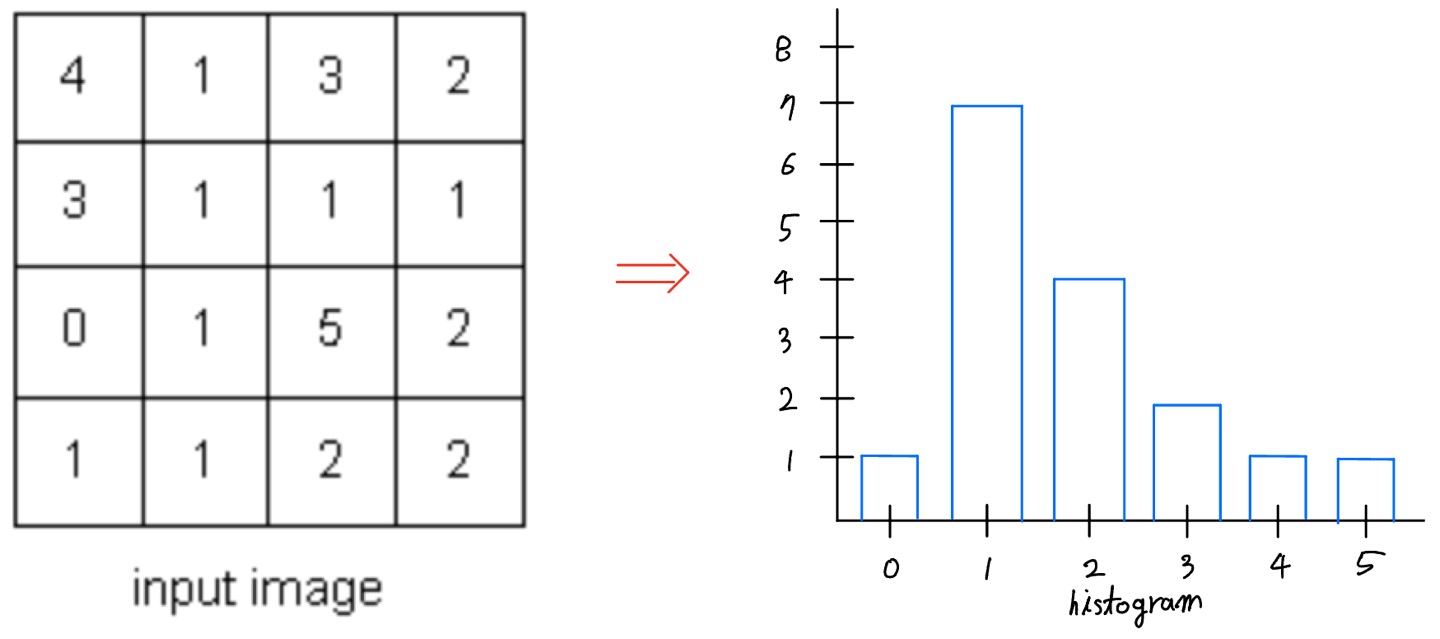
input_image

위 그림과 같이 M과 N이 4이고 L=6인 아주 작은 영상이 있습니다. 이 영상에서 1인 화소는 7개이므로 $h(1)=7$이고, 나머지 화소의 개수를 세어보면 input image의 히스토그램은 $h = (1, 7, 4, 2, 1, 1)$이고, 이때 히스토그램 $h$를 정규화한 히스토그램의 값은 $\hat{h} = (\frac{1}{16}, \frac{7}{16}, \frac{4}{16}, \frac{2}{16}, \frac{1}{16}, \frac{1}{16}) = (0.0625, 0.4375, 0.25, 0.125, 0.0625, 0.0625)$ 으로 나오게 됩니다.

Histogram Equalization Calculation

$l_{out} = T(l_{in}) = round(c(l_{out})\times(L-1))$

이때 $c(l_{in}) = \sum_{l=0}^{l_{in}}\hat{h}(l)$

위 식을 토대로 구하면 아래와 같은 값들을 구할 수 있습니다.

$l_{in}$ $\hat{h}(l_{in})$ $c(l_{in})$ $c(l_{in})\times5$ $l_{out}$
0 0.0625 0.0625 0.3125 0
1 0.4375 0.5 2.5 3
2 0.25 0.75 3.75 4
3 0.125 0.875 4.375 4
4 0.0625 0.9375 4.6875 5
5 0.0625 1.0 5 5

구해진 값들로 다시 히스토그램을 만들어 보면 아래 사진과 같이 히스토그램이 평활화 된 것을 확인 할 수 있습니다.

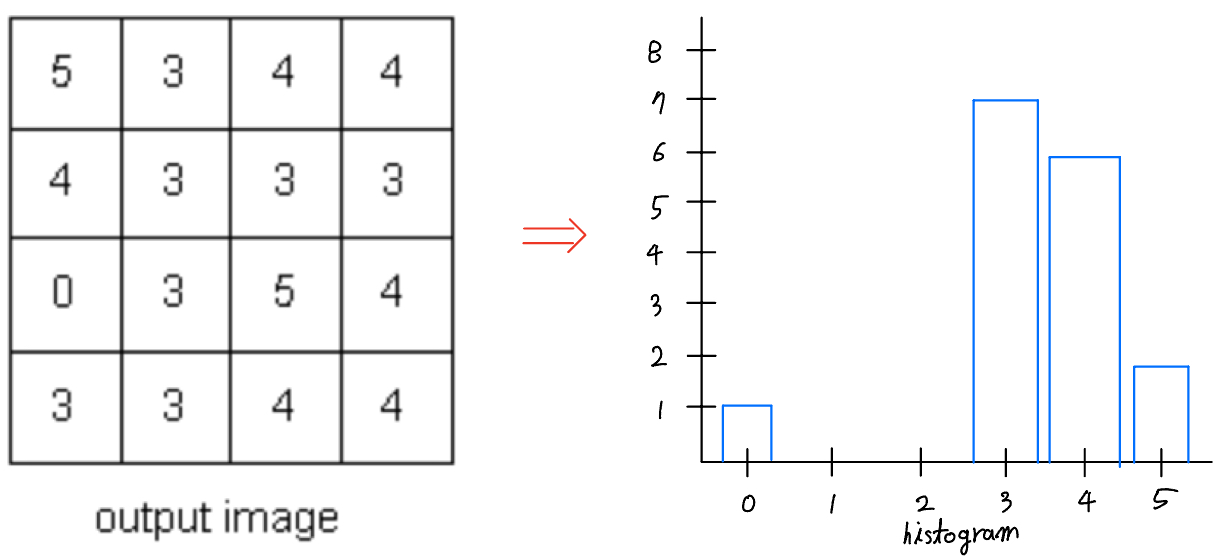
output_image

이런 히스토그램 평활화를 사용하면 이미지의 전반적인 대비를 향상시켜, 기존 이미지의 비해 뚜렷한 대비를 강조할 수 있게 됩니다.

Effect of Histogram Equalization

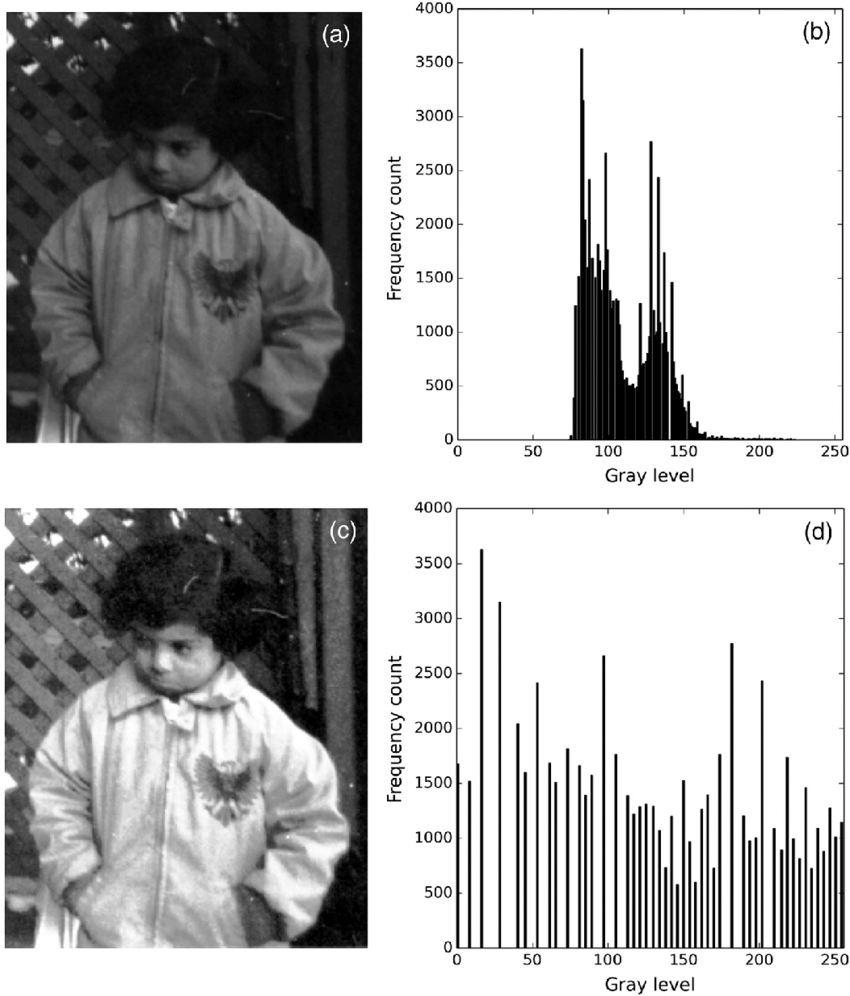
example

기존 이미지(a)의 비해 히스토그램 평활화가 된 이미지(c)가 기존 이미지의 비해 뚜렷한 대비를 가지고 있는 것을 확인 할 수 있습니다.

하지만 아래 사진과 같이 항상 모든 이미지에 대해서 좋은 결과가 나오는 것은 아니기 때문에 잘 확인해야한다.

bad_example

Python Code

# load image
input_color_img = cv2.imread("/content/drive/MyDrive/Computer_Vision/data/mistyroad.jpeg")
height, width, _ = input_color_img.shape
input_gray_img = cv2.cvtColor(input_color_img, cv2.COLOR_BGR2GRAY)

cv2_imshow(input_gray_img)

# gray scale에서 각각의 픽셀은 0~255까지의 값들을 가지게 때문에 다음과 같은 numpy 리스트를 만들어준다.
histogram = np.zeros((256))

# 반복문을 돌면서 각각의 픽셀이 가지는 값마다 개수를 카운팅한 후 histogram list에 저장
for i in range(height):
    for j in range(width):
        histogram[int(input_gray_img[i][j])] += 1

# input 이미지, 히스토그램 출력
import matplotlib.pyplot as plt
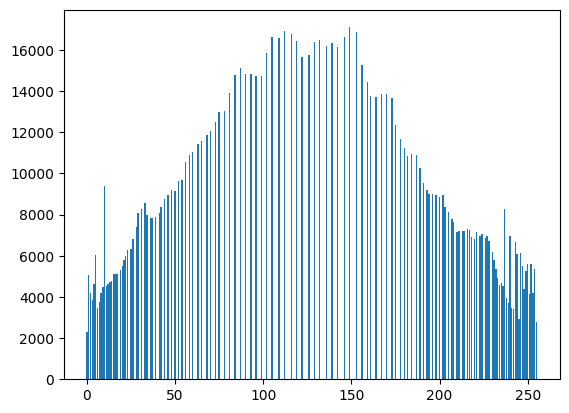
plt.bar(range(len(histogram)), histogram)

​
image_1 ​

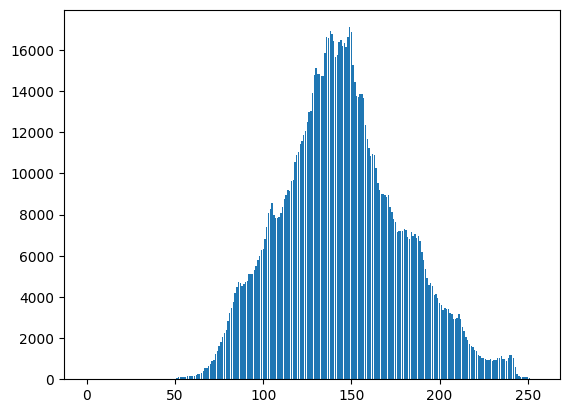
hist_1 ​

아래 코드는 cv2 내장 함수를 사용하지 않고 히스토그램 평활화 공식을 사용하여 직접 구현

clin = 0
equalizedHist = np.zeros((256))
hisMatch = np.zeros((256))
for i in range(len(histogram)):
  clin += histogram[i]
  hisMatch[i] = round(clin / (912*1368) * 255)

for i in range(height):
    for j in range(width):
        input_gray_img[i][j] = hisMatch[input_gray_img[i][j]]

for i in range(height):
    for j in range(width):
        equalizedHist[int(input_gray_img[i][j])] += 1

plt.bar(range(len(equalizedHist)), equalizedHist)

equalizedimg = np.zeros((height,width), dtype=np.uint8)
for i in range(height):
    for j in range(width):
        equalizedimg[i][j] = hisMatch[input_gray_img[i][j]]

cv2_imshow(equalizedimg)

image_2 ​

hist_2

아래 코드는 cv2 내장함수 사용

dst = cv2.equalizeHist(input_gray_img)
hist = cv2.calcHist([dst], [0], None, [256], [0,256])
cv2_imshow(dst)
plt.bar(range(len(hist.reshape(256))), hist.reshape(256))

image_3 ​

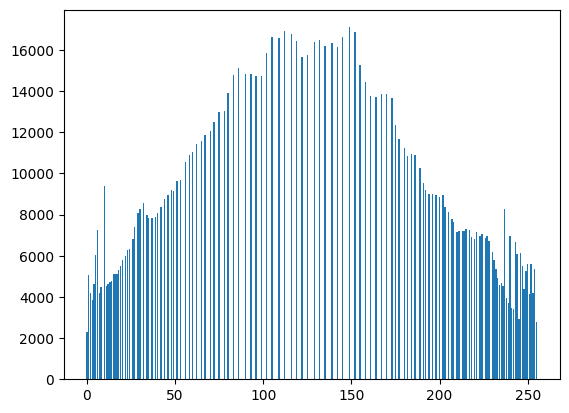
hist_3


결과를 보면 히스토그램 평활화를 사용함으로서 대비가 더 뚜렷해지는 것을 확인 할 수 있습니다.

참고